Section 2.5 The transpose and trace of a matrix
Definition 2.5.1. The transpose of a matrix.
The transpose of \(A\) is the matrix \(A^T\) derived by making the first row of \(A\) the first column of \(A^T\text{,}\) the second row of \(A\) the second column of \(A^T\text{,}\) etc. In other words, when taking a transpose, the rows and columns are interchanged. Another way of saying this is that the subscripts have been interchanged, that is, if \(A^T=B=[b_{i,j}].\) then \(b_{i,j}=a_{j,i}\)
Example 2.5.2. Matrix transposes.
Let \(A=\begin{bmatrix} 1\amp2\amp3\\4\amp5\amp6\\7\amp8\amp9 \end{bmatrix}.\) Then \(A^T=\begin{bmatrix} 1\amp4\amp7\\2\amp5\amp8\\3\amp6\amp9 \end{bmatrix}\)
The identity matrix \(I_n\) of order n has all diagonal entries equal to one and all other entries equal to zero. \(I_n=\begin{bmatrix} 1 \amp 0 \amp 0 \amp \cdots \amp 0\\ 0 \amp 1 \amp 0 \amp \cdots \amp 0\\ 0 \amp 0 \amp 1 \amp \cdots \amp 0\\ \amp \amp \amp \ddots \amp \\ 0 \amp 0 \amp 0 \amp \cdots \amp 1 \end{bmatrix}_n\) Clearly \(I_n^T=I_n.\)
The transpose is defined for nonsquare matrices, too. Let \(A=\begin{bmatrix} 1 \amp 2 \amp 3 \amp 4 \\ 5 \amp 6 \amp 7 \amp 8 \\ 9 \amp10\amp11\amp12 \end{bmatrix}.\) Then \(A^T=\begin{bmatrix} 1 \amp 5 \amp9\\ 2 \amp 6 \amp 10\\ 3 \amp 7 \amp 11\\ 4 \amp 8 \amp 12 \end{bmatrix}.\)
Here is an animation that illustrates that \(A^T\) may be derived from \(A\) by reflection on the main diagonal.
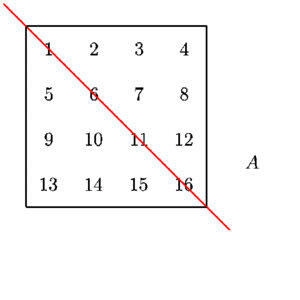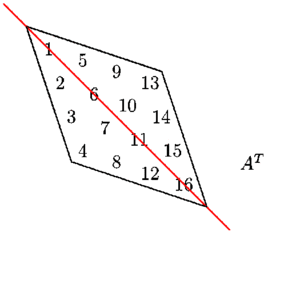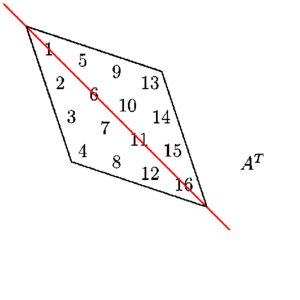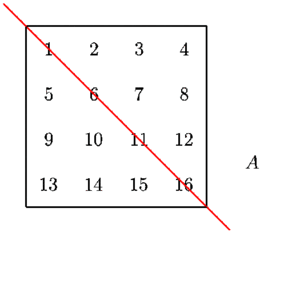
Theorem 2.5.4. Properties of the transpose of a matrix.
\(\displaystyle (A^T)^T=A\)
\(\displaystyle (A+B)^T=A^T+B^T\)
\(\displaystyle (rA)^T=rA^T\)
\(\displaystyle (AB)^T=B^TA^T\)
Proof.
The \(i\)-\(j\) entry of \(A^T\) is \(a_{j,i}\text{,}\) obtained by interchanging the subscripts of \(A\text{.}\) Taking the transpose again interchanges the subscripts again, and so the \(i\)-\(j\) entry of \((A^T)^T\) is \(a_{i,j}\text{,}\) the same as for \(A\text{.}\) Hence \((A^T)^T=A\text{.}\)
The \(i\)-\(j\) entry on both sides of the equation is \(a_{j,i}+b_{j,i}\text{.}\)
The \(i\)-\(j\) entry on both sides of the equation is \(ra_{j,i}`\text{.}\)
-
The \(i\)-\(j\) entry of \((AB)^T\) is the \(j\)-\(i\) entry of \(AB,\) which in turn is
\begin{equation*} a_{j,1}b_{1,i} +a_{j,2}b_{2,i}+\cdots +a_{j,n}b_{n,i}. \end{equation*}The \(i\)-\(j\) entry of \(B^TA^T\) is \((B^T)_{i,1}(A^T)_{1,j} + (B^T)_{i,2}(A^T)_{2,j} +\cdots + (B^T)_{i,n}(A^T)_{n,j} =\\ b_{1,i}a_{j,1} + b_{2,i}a_{j,2} +\cdots + b_{n,i}a_{j,n}.\) Hence both sides of the equation have the same \(i\)-\(j\) entry, and so the matrices are equal.
Proof.
Definition 2.5.5. Trace of a square matrix.
The trace of a square matrix \(A\) of size \(n\) is the sum of the diagonal elements, that is,
Theorem 2.5.6. Traces of \(AB\) and \(BA\) are equal.
If \(AB\) and \(BA\) are each square, then \(\tr (AB)=\tr (BA)\)
Proof.
Suppose that \(A\) is \(m\times n\) and \(B\) is \(n\times m\) (remember that \(AB\) is then defined and square). To evaluate both \(\tr (AB)\) and \(\tr (BA)\text{,}\) we consider the following rectangular array of numbers:
We are going to compute the sum of all the elements of this array in two ways. Having done this, the two answers will be equal.
First we find the sum of all the entries of the array by adding row-wise. Observe that the sum of the elements in the first row is \((AB)_{1,1}\text{,}\) the sum of those in the second row is \((AB)_{2,2}\text{,}\) and so on until the sum of the elements in the last row is \((AB)_{m,m}\text{.}\) Hence the sum of all of the elements in the array is \((AB)_{1,1}+(AB)_{2,2}+\cdots+(AB)_{m,m}=\tr (AB)\text{.}\)
Now we add columnwise. Notice that the first column sums to
the second column sums to \((BA)_{2,2}\) and so on until the last column sums to \((BA)_{n,n}\text{.}\)Hence the sum of all of the elements in the array is \((BA)_{1,1}+(BA)_{2,2}+\cdots+(BA)_{n,n}=\tr (BA)\text{.}\) Equating the two evaluations gives \(\tr (AB)=\tr (BA)\text{.}\)
Proof.
Suppose that \(A\) is \(m\times n\text{.}\) Then, since \(AB\) and \(BA\) are defined, the conformability ensures that \(B\) is \(n\times m\text{.}\)
