Cross Product of Vectors in \(\R^3\)

Section 4.5 Cross Product of Vectors in \(\R^3\)

Subsection 4.5.1 Definition of the cross product

The cross product is only defined for vectors in \(\R^3\text{.}\) Given two such vectors \(\vec x=(x_1,x_2,x_3)\) and \(\vec y=(y_1,y_2,y_3)\text{,}\) the cross product \(\vec x\times\vec y\) is a vector in \(\R^3\) defined by

\begin{equation*} \vec x\times\vec y = (x_2y_3-x_3y_2,\, x_3y_1-x_1y_3,\,x_1y_2-x_2y_1) \end{equation*}

This is pretty complicated and, as yet, unmotivated. Here is a neat trick to make the computation a little easier. Take the two vectors and make an array by writing the three coordinates and then repeating the first two coordinates again:

\begin{equation*} \begin{matrix} x_1\amp x_2\amp x_3\amp x_1\amp x_2\\ y_1\amp y_2\amp y_3\amp y_1\amp y_2 \end{matrix} \end{equation*}

We then use three “sliding windows”: the first (for the first coordinate) uses columns two and three, the next (for the second coordinate) uses columns three and four, and the last (for the third coordinate) uses columns four and five.

First coordinate: \(\color{red}{x_2y_3}-\color{green}{x_3y_2}\)

\begin{equation*} \begin{matrix} \begin{matrix} x_1\\y_1 \end{matrix} \begin{bmatrix} \color{red}{x_2} \amp \color{green}{x_3}\\ \color{green}{y_2} \amp \color{red}{y_3} \end{bmatrix} \begin{matrix} x_1 \amp x_2\\ y_1 \amp y_2 \end{matrix} \end{matrix} \end{equation*}
Second coordinate: \(\color{red}{x_3y_1}-\color{green}{x_1y_3}\)

\begin{equation*} \begin{matrix} \begin{matrix} x_1 \amp x_2\\ y_1 \amp y_2 \end{matrix} \begin{bmatrix} \color{red}{x_3} \amp \color{green}{x_1}\\ \color{green}{y_3} \amp \color{red}{y_1} \end{bmatrix} \begin{matrix} x_2\\y_2 \end{matrix} \end{matrix} \end{equation*}
Third coordinate: \(\color{red}{x_1y_2}-\color{green}{x_2y_1}\)

\begin{equation*} \begin{matrix} \begin{matrix} x_1\amp x_2\amp x_3\\ y_1\amp y_2\amp y_3 \end{matrix} \begin{bmatrix} \color{red}{x_1} \amp \color{green}{x_2}\\ \color{green}{y_1} \amp \color{red}{y_2} \end{bmatrix} \end{matrix} \end{equation*}

In each case the window is evaluated by

\begin{equation*} (\textrm{upper left})(\textrm{lower right}) -(\textrm{upper right})(\textrm{lower left}) \end{equation*}

which is actually the determinant as seen in Definition 3.1.1.

Here is an animation showing two vectors (the blue vectors) and their cross product (the red vector):

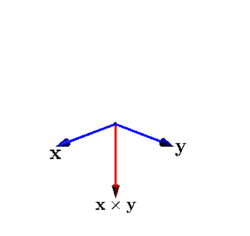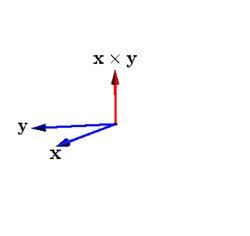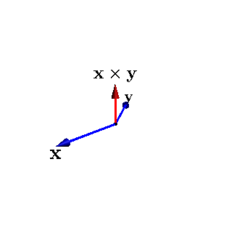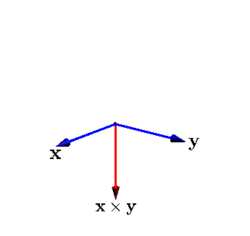
There are (at least) four interesting relationships between the two blue vectors and their cross product.

Can you see some of them? Press to reveal:

Example 4.5.2. Interesting properties of the cross product.

\(\vec x\times\vec y\) is perpendicular to both \(\vec x\) and \(\vec y\text{.}\)
\(\vec x\times\vec y\) has zero length when \(\vec x\) and \(\vec y\) are collinear.
\(\vec x\times\vec y\) has maximum length when \(\vec x\) and \(\vec y\) are perpendicular.
As \(\vec y\) goes through one cycle around \(\vec x\text{,}\) the length of \(\vec x\times\vec y\) goes up and down like the function \(\sin(x)\text{.}\)

These relationships are all valid, as we now show.

Theorem 4.5.3. \(x\perp\vec x\times\vec y\) and \(y\perp\vec x\times\vec y\).

\(\vec x\times\vec y\) is perpendicular to both \(\vec x\) and \(\vec y\text{.}\)

Proof.

The desired result is shown if \(\vec x\cdot(\vec x\times\vec y)=0\) and \(\vec y\cdot(\vec x\times\vec y)=0\text{.}\) By direct computation

\begin{equation*} \begin{array}{rl} (x_1,x_2,x_3) \cdot \amp(x_2y_3-x_3y_2, x_3y_1-x_1y_3,x_1y_2-x_2y_1)\\ \amp=x_1 (x_2y_3-x_3y_2) +x_2 (x_3y_1-x_1y_3) + x_3 (x_1y_2-x_2y_1)\\ \amp= x_1x_2y_3-x_1x_3y_2 +x_2 x_3y_1-x_2x_1y_3+ x_3x_1y_2-x_3x_2y_1\\ \amp=0 \end{array} \end{equation*}

and

\begin{equation*} \begin{array}{rl} (y_1,y_2,y_3) \amp\cdot (x_2y_3-x_3y_2, x_3y_1-x_1y_3,x_1y_2-x_2y_1)\\ \amp=y_1 (x_2y_3-x_3y_2) +y_2 (x_3y_1-x_1y_3) + y_3 (x_1y_2-x_2y_1)\\ \amp= y_1x_2y_3-y_1x_3y_2 +y_2 x_3y_1-y_2x_1y_3+ y_3x_1y_2-y_3x_2y_1\\ \amp=0 \end{array} \end{equation*}

Theorem 4.5.4. \(\vec x \times r\vec x=\vec0\).

If \(\vec x\) and \(\vec y\) are collinear, then \(\vec x\times\vec y=\vec 0\text{.}\)

Proof.

The collinearity of \(\vec x\) and \(\vec y\) means that \(\vec x=r\vec y\) for some real number \(r\text{,}\) and so \(x_1=ry_1\text{,}\) \(x_2=ry_2\text{,}\) and \(x_3=ry_3\text{.}\) This means

\begin{equation*} \begin{array}{rl} \vec x\times\vec y \amp= (ry_1,ry_2,ry_3)\times(y_1,y_2,y_3)\\ \amp= (ry_2y_3-ry_3y_2, ry_3y_1-ry_1y_3,ry_1y_2-ry_2y_1)\\ \amp=(0,0,0)=\vec 0 \end{array} \end{equation*}

Now we carry out some computations:

\begin{align*} \|\vec x\times\vec y\|^2 \amp=\|(x_2y_3-x_3y_2, x_3y_1-x_1y_3, x_1y_2-x_2y_1)\|^2\\ \amp= x_2^2y_3^2 - 2x_2x_3y_2y_3 + x_3^2y_2^2\\ \amp\quad+x_3^2y_1^2 - 2x_1x_3y_1y_3 + x_1^2y_3^2\\ \amp\quad+x_1^2y_2^2 - 2x_1x_2y_1y_2 + x_1^2y_2^2\\ \|\vec x\|^2 \|\vec y\|^2 \amp=x_1^2y_1^2 + x_1^2y_2^2 + x_1^2y_3^2\\ \amp=+ x_2^2y_1^2 +x_2^2y_2^2 + x_2^2y_3^2\\ \amp\quad+x_3^2y_1^2 +x_3^2y_2^2 + x_3^2y_3^2\\ (\vec x\cdot\vec y)^2 \amp=(x_1y_1+x_2y_2+x_3y_3)^2\\ \amp= x_1^2y_1^2+x_2^2y_2^2+x_3^2y_3^2 +2 x_1x_2y_1y_2 +2x_1x_3y_1y_3 +2 x_2x_3y_2y_3 \end{align*}

Upon careful examination we conclude

\begin{equation*} \|\vec x\times\vec y\|^2 + (\vec x\cdot\vec y)^2 = \|\vec x\|^2 \|\vec y\|^2 \end{equation*}

Theorem 4.5.5. \(\|\vec x\times\vec y\|=\|\vec x\|\,\|\vec y\|\sin\theta\).

For any vectors \(\vec x\) and \(\vec y\) in \(\R^3\text{,}\) \(\|\vec x\times\vec y\|=\|\vec x\|\,\|\vec y\|\sin\theta\text{.}\)

Proof.

\begin{equation*} \begin{array}{rl} \|\vec x\times\vec y\|^2 \amp= \|\vec x\|^2\|\vec y\|^2 -(\vec x\cdot\vec y)^2 \\ \amp= \|\vec x\|^2 \|\vec y\|^2 -\|\vec x\|^2\|\vec y\|^2\cos^2(\theta) \\ \amp= \|\vec x\|^2\|\vec y\|^2(1-\cos^2(\theta))\\ \amp= \|\vec x\|^2\|\vec y\|^2\sin^2(\theta) \end{array} \end{equation*}

Taking the square root of both sides, we get

\begin{equation*} \|\vec x\times\vec y\| =\pm \|\vec x\|\, \|\vec y\| |\sin(\theta)| \end{equation*}

Now \(\|\vec x\times\vec y\|\geq 0\text{,}\) that is, the left side of the equation is nonnegative. Also \(\|\vec x\|\, \|\vec y\|\geq 0\text{.}\) In addition, \(\sin(\theta)\geq 0\) for \(0\leq \theta \leq \pi\text{.}\) This means that to make the right side of the equation nonnegative, the \(\pm\) is actually \(+\text{.}\) Hence

\begin{equation*} \|\vec x\times\vec y\| =\|\vec x\|\, \|\vec y\| \sin(\theta) \end{equation*}

Theorem 4.5.6. Additional cross product properties.

Let \(\vec u\) and \(\vec v\) be vectors in \(\R^n\text{,}\) and let \(r\) be a real number. Then

\(\displaystyle \vec u\times\vec v=-(\vec v\times\vec u)\)
\(\displaystyle (r\vec u)\times\vec v=r(\vec u\times\vec v)\)
\(\displaystyle \vec u \times (\vec v+\vec w) =(\vec u \times \vec v)+(\vec u\times\vec w)\)

Proof.

All of the parts may be verified by direct computation. But more easily:

\(\displaystyle \det \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ u_1 \amp u_2 \amp u_3\\ v_1 \amp v_2 \amp v_3 \end{bmatrix} =- \det \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ v_1 \amp v_2 \amp v_3\\ u_1 \amp u_2 \amp u_3 \end{bmatrix}\)
\(\displaystyle \det \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ ru_1 \amp ru_2 \amp ru_3\\ v_1 \amp v_2 \amp v_3 \end{bmatrix} =r \det \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ u_1 \amp u_2 \amp u_3\\ v_1 \amp v_2 \amp v_3 \end{bmatrix}\)
\(\displaystyle \det \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ u_1 \amp u_2 \amp u_3\\ (v_1+w_1) \amp (v_2+w_2) \amp (v_3+w_3) \end{bmatrix} = \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ u_1 \amp u_2 \amp u_3\\ v_1 \amp v_2 \amp v_3 \end{bmatrix} + \begin{bmatrix} \vec i \amp \vec j\amp \vec j\\ u_1 \amp u_2 \amp u_3\\ w_1 \amp w_2 \amp w_3 \end{bmatrix}\)

Justification of the definition of the cross product.

Now suppose we have two vectors \(\vec x=(x_1,x_2,x_3)\) and \(\vec y=(y_1,y_2,y_3)\text{.}\) We are looking for a third vector which (like the cross product) is perpendicular to both \(\vec x\) and \(\vec y\text{.}\) Let's call such a vector \((a,b,c)\text{.}\) The perpendicularity assumptions mean \((a,b,c)\cdot(x_1,x_2,x_3)=0\) and \((a,b,c)\cdot(y_1,y_2,y_3)=0\text{.}\) This means \(\begin{align*} ax_1+bx_2+cx_3\amp =0\tag{1}\\ ay_1+by_2+cy_3\amp =0.\tag{2} \end{align*}\)

Multiply equation \((1)\) by \(y_1\text{,}\) equation \((2)\) by \(x_1\) and subtract. This gives

\begin{equation*} b(x_2y_1-x_1y_2)+c(x_3y_1-x_1y_3)=0 \end{equation*}

and so

\begin{equation*} b=\frac{x_3y_1-x_1y_3}{x_1y_2-x_2y_1}c \end{equation*}

Now multiply equation \((1)\) by \(y_2\text{,}\) equation \((2)\) by \(x_2\) and subtract.

This gives

\begin{equation*} a(x_1y_2-x_2y_1)+c(x_3y_2-x_2y_3)=0 \end{equation*}

and so

\begin{equation*} a=\frac{x_2y_3-x_3y_2}{x_1y_2-x_2y_1}c \end{equation*}

This implies that our vector

\begin{equation*} (a,b,c)=\left(\frac{x_2y_3-x_3y_2}{x_1y_2-x_2y_1}c, \frac{x_3y_1-x_1y_3}{x_1y_2-x_2y_1}c,c\right) \end{equation*}

is perpendicular to both \(\vec x\) and \(\vec y\) for any choice of \(c\text{.}\) If we set \(c=x_1y_2-x_2y_1\) then we get

\begin{equation*} (a,b,c)=(x_2y_3-x_3y_2,x_3y_1-x_1y_3,x_1y_2-x_2y_1) \end{equation*}

which is precisely \(\vec x\times\vec y\text{.}\) Hence the definition of the cross product, which at first seems bizarre, is actually natural if we wish the product to be perpendicular to both of the factors.